Matrix Multiplication Commutative Example
Here the matrices are each 2 x 2 and so the result will be a 2 x 2 matrix. Its submitted by paperwork in the best field.

Learn Matrix Multiplication Using Either Of Gradea S Easy To Use Methods The Turn And Flip Or The Zipper Met Matrix Multiplication Matrices Math Studying Math
Matrix multiplication is associative.
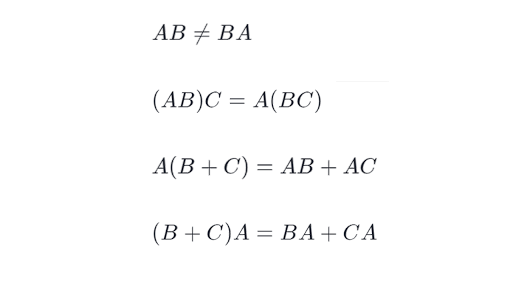
Matrix multiplication commutative example. In the real numbes addition is commutative. 3 The matrices given are rotation matrices. It is also commutative if a matrix is multiplied with the identity matrix.
12 16 4 0 36 20 12 16 4 0 36 20 This is the required matrix after multiplying the given matrix by the constant or scalar value ie. Most commonly a matrix over a field F is a rectangular array of scalars each of which is a member of F. For example given 3 matrices A B and C the following identity is always true But since we already said that matrix multiplication is not commutative the following is NOT true or any other permutation of the sort.
It is a fact that matrix multiplication is NOT commutative in general. Matrix multiplication is commutative when a matrix is multiplied with itself. A B I inv AA B inv A Premultiplying both sides by inv A inv AA B A inv AA Postmultiplying both sides by A B A I Canceling inverses QED There are lots of special cases that commute.
The matrices must maintain their order. Matrix multiplication follows the distributive property ie multiplication of matrix A and matrix B with. For any two real numbers a b b a.
Example Find the product AB where. Here are a number of highest rated Matrix Multiplication Commutative pictures upon internet. For example this always works when Ais the zero matrix or when AB.
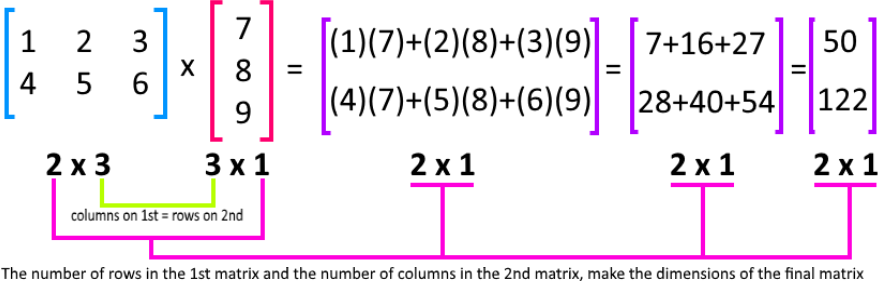
Now that we have seen some of the important properties of matrix multiplication lets work through a couple of examples. The reader is encouraged to find other examples. Given A 3 4 1 0 9 5 A 3 4 1 0 9 5 4 A 43 4 1 0 9 5 4 3 4 1 0 9 5 Now we have to multiply each element of the matrix A by 4.
Matrix multiplication is non-commutative ie for multiplication of two matrices A and B AB BA. While matrix multiplication is not commutative in general there are examples of matrices Aand Bwith ABBA. A 5 3 4 1 and B 1 1 2 6 Solution Remember that rows hit columns and fill up rows.
Therefore matrix multiplication is not commutative. We can multiply a number aka. For any two real numbers ab.
1 One of the given matrices is an identity matrix. GATE 1996 Discrete and Engineering Mathematics Linear AlgebraThe matricescostheta -sinthetasintheta costhetaANDa 00 bcommute under multip. Even though matrix multiplication is not commutative it is associative in the following sense.
Scalar by a matrix by multiplying every entry of the matrix by the scalar this is denoted by juxtaposition or with the scalar on the left. This means that we may get a different result depending on the order in which the matrices are multiplied that is ABBA. Matrix multiplication can be commutative in the following cases.
ExampleNon-commutative multiplication of matrices Order of Operations. If A is a matrix then AA A2 AA. 2 1 6 9 3 6 0 2 12 18 6 12 0 sometimes you see scalar multiplication with the scalar on the right α βA αAβA.
Hence AB BA. Since these expressions may very well not be equal according to our work thus far we can safely conclude that matrix multiplication is not necessarily commutative. When you multiply a matrix with the identity matrix the.
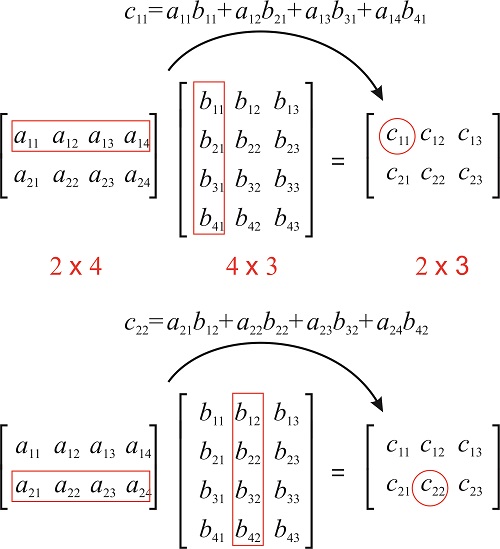
For the example above the 32-entry of the product AB is given by beginbmatrix 4 0 endbmatrix beginbmatrix 1 3endbmatrix 4. B21 b22 b23. Matrix Multiplication is distributive across addition.
A real matrix and a complex matrix are matrices whose entries are respectively real numbers or complex numbers. We identified it from well-behaved source. Was this answer helpful.
A13 a23 a33 b21 a13 b22 a23 b23 a33 If matrix multiplication were commutative we would expect BA23 AB23 among other things. Matrix multiplication is associative. 8 2 16 blueD8 times purpleD2 pink 16 8216.
A matrix is a rectangular array of numbers or other mathematical objects for which operations such as addition and multiplication are defined. The commutative property is a math rule that says that the order in which we multiply numbers does not change the product. In this video we explore whether matrix multiplication is commutative or whether it really does matter in which order we multiply 2 matricesIn the first exa.
2 One of the given matrices is a zero matrix. αβA αβA αABαAαB. See also what was a major result of the civil war.
There are special kinds of matrices called. 4 The matrices given are diagonal matrices. ANY two square matrices that are inverses of each other commute.
There are certain properties of matrix multiplication operation in linear algebra in mathematics. We take this kind of Matrix Multiplication Commutative graphic could possibly be the most trending subject subsequently we portion it in google lead or facebook. These properties are as given below Non-Commutative.
15 3 Matrix Multiplication Chemistry Libretexts

Multiplication Of Matrices Multiplication Matrix Multiplication Matrix

Understanding Affine Transformations With Matrix Mathematics Math Methods Learning Mathematics Affine Transformation

Algebra 2 Worksheets Dynamically Created Algebra 2 Worksheets Word Problem Worksheets Matrices Math Algebra 2 Worksheets

Matrix Multiplication Examples How To Multiply Matrices

Multiplying Matrices Mathbootcamps

Matrix Multiplication Examples How To Multiply Matrices

Scalar And Matrix Multiplication Matrix Multiplication Matrices Math Multiplying Matrices
Properties Of Matrix Multiplication Article Khan Academy

Arithmetic Properties Commutative Associative Distributive Associative Property Math Properties Commutative

Introduction To Matrices Includes The Following Foldable Activities What Is A Matrix What Ar Matrices Math Interactive Notebook Activities Teaching Algebra
Properties Of Matrix Multiplication Studypug
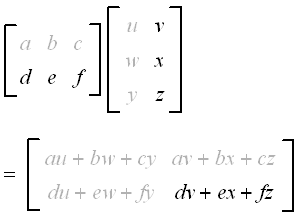
Posting Komentar untuk "Matrix Multiplication Commutative Example"