Simplifying Radicals With Negative Radicands
Simplifying radicals solve How to calculate scale factor 6th grade Passport math7th grade lesson 76. For example you know that 2 2 4.

How Do You Simplify The Square Root Of A Negative Number Printable Summary Virtual Nerd
Negative a Graphing and Writing Equations of Hyperbolas.
Simplifying radicals with negative radicands. Writing radicals with rational exponents will come in handy when we discuss techniques for simplifying more complex radical expressions. The principal square root is the nonnegative number that when multiplied by itself equals a. Radicand - The number inside the radical.
To multiply radicands multiply the numbers as if they were whole numbers. Thus the number -6 can be a square root of the number 36 just not a principal square root. Just like exponentiation is repetitive multiplication taking a root from a number is repetitive division.
PRODUCT PROPERTY OF SQUARE ROOTS For all real numbers a and b a b a b That is the square root of the product is the same as the product of the square roots. If we take Warm up question 1 and put a 6 in front of it it looks like this. The square root of a negative number results in.
Essentially a monomial is a single term with a coefficient and to non-negative a whole number possibly zero power. Com provides good material on simplifying square root calculator line and rational functions and other math topics. Kuta software infinite algebra 2 name radicals and rational exponents date period write each expression in radical form.
1-7 The Distributive Property 7-1 Zero and Negative Exponents 8-2 Multiplying and Factoring 10-2 Simplifying Radicals 11-3 Dividing Polynomials 12-7 Theoretical and Experimental Probability Absolute Value Equations and. Students will practice simplifying radicals. To simplify sqrt2-1 Oct 25 2012 For example if a 3 and a 2 are flipped over then the players would race to simplify the square root of 32.
Addition and subtraction of two or more radicals can be performed with like radicals and like radicands only. Root index must be. Explore an overview of square roots with a definition of the negative square root learn about the imaginary unit.
Where n is a positive integer sometimes called the degree of the root. In mathematics an nth root of a number x is a number r which when raised to the power n yields x. Simplifying Radical Expressions Before you can simplify a radical expression you have to know the important properties of radicals.
If you have buttons exp and ln tyope the number then ln multiply by 0. Radicals of different indices and different radicands are called dissimilar radicals. Although square roots are the most common rational roots we can also find cube roots 4th roots 5th roots and more.
93 43 13 3. Back to Complex Numbers Home Next to Negative Radicals. Negative exponents for beginners polynomials subtraction worksheets linear regression parigp using algebraic expressions investigation ks3 printable ks3 science sats paper.
Answer the next activity that deals with this understanding. Make sure to keep the product under one radical sign. If there are coefficients multiply them together as well.
Simplifying radicals with fractions modern algebra done exercise free Easy way to find LCM online prealgebra worksheets. Not Perfect Cube Radicands Simplifying Radical Expressions Without Fractions. Radicals is an opposite action from exponentiation.
Because the numbers inside the square roots are same. The square root obtained using a calculator is the principal square root. This section introduces two types of radicands with variables and covers how to simplify them.
The Hyperbola part 1 of 2 Conic Sections. Rationalizing the Denominator To rationalize the denominator means to eliminate any radical expressions in the denominator such as square roots and cube roots. Practice Problems Problem 1 i 23.
Test of Genius discrete math worksheet 9th grade Texas TAKS worksheets 4th grade volume worksheet algebra elementary 5th download introductory to algebra blitzer intermediate algebra multiple choice rational. In this lesson we will only focus on square. A root of degree 2 is called a square root and a root of degree 3 a cube rootRoots of higher degree are referred by using ordinal numbers as in fourth root twentieth root etc.
The key idea is to multiply the original fraction by an appropriate value such that after simplification the denominator no longer contains radicals. If you want to take second also called square root from number 4 is number 2. Sqrt-18.
Ultimate Math Solver Free Free Algebra. So the negative square root is the same number as the principal square root but the negative version. Radicals and radicands graph.
A radicand is a number underneath the radical sign. For example if we input 8 in a calculator the calculator would display 2828427124746190097603377448419. If the indices or radicands are not the same then you can not add or subtract the radicals.
93 - 4. If the indices and radicands are the same then add or subtract the terms in front of each like radical. A negative square root and a positive square root make a positive number.
To add or subtract radicals the indices and what is inside the radical called the radicand must be exactly the same. Radical expressions come in many forms from simple and familiar such aslatex sqrt16latex to quite complicated as in latex sqrt3250. 3 2 5 2 6 54 - - 10 63 - 6 2 - 10 2 5 63 24 2 - 20 63 - Questions.
For example 93 and 43 can be added or subtracted. Like radicals - Radicals with the same index. Puzzle-Math Perform the indicated operations as you complete the puzzle below.
3 or 4 the key to simplifying powers of i is the remainder when the exponent is divided by 4. Multiply the radicands. The computation of an n th root is.
Simplifying radicals with variables follows the same rules as one that only has numbers. Radical expressions are expressions that contain radicals. The Hyperbola part 2 of 2.
The principal square root of a a is written as a. SIMPLIFY RADICALS WITH NO PERFECT ROOT Not all radicands are perfect squares where when we take the square root we obtain a positive integer. In order to multiply radicals containing variables the.
Simplifying Radicals Simplify Square Roots Perfect Square Radicands. Simplifying Radicals with Coefficients When we put a coefficient in front of the radical we are multiplying it by our answer after we simplify. Simplifying negative radicands sqrt-25.
The square root could be positive or negative because multiplying two negative numbers gives a positive number. This section discusses how to handle type two radicals. Just as the square root function is the inverse of the squaring function these roots are the inverse of their respective power functions.
Second uses two square root sign are easy for the radicand in the answer a Simplifying Radicals Search. In addition to numbers radicals can contain other things like variables and exponents. Simplifying radical expressions pdf answers.

5 Ways To Simplify Radical Expressions Wikihow

5 Ways To Simplify Radical Expressions Wikihow

5 Ways To Simplify Radical Expressions Wikihow
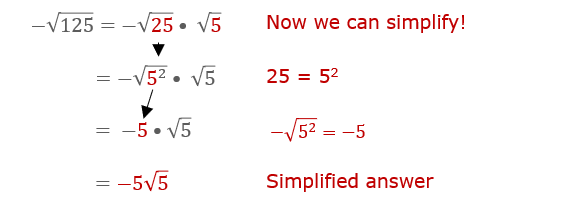
Learn How To Simplify A Square Root In 2 Easy Steps
How To Simplify Square Roots Review Article Khan Academy

How Do You Simplify The Square Root Of A Negative Number Virtual Nerd

5 Ways To Simplify Radical Expressions Wikihow

Square Roots Of Negative Numbers Youtube

5 Ways To Simplify Radical Expressions Wikihow

Simplifying Radical Expressions

Simplifying Radical Expressions

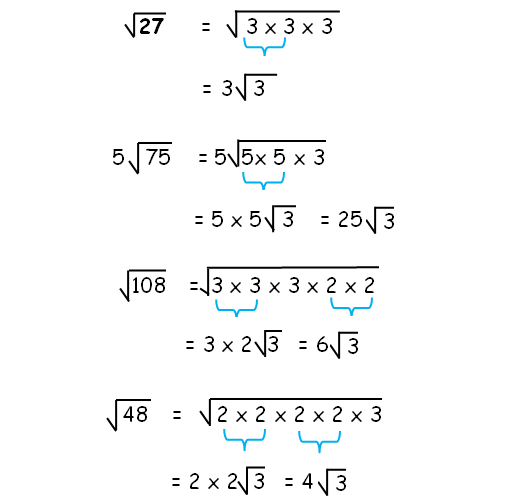
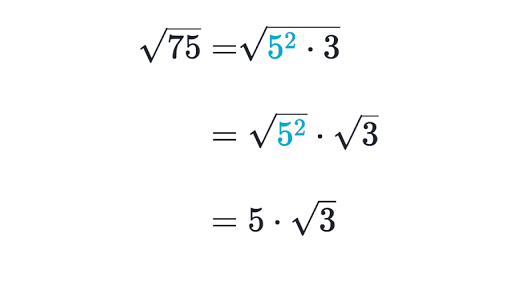
Posting Komentar untuk "Simplifying Radicals With Negative Radicands"